DFS(깊이우선탐색)는 BFS와 함께 대표적으로 사용되는 그래프 탐색 알고리즘 중 하나다.
DFS의 탐색 과정은 한마디로 표현하자면 '끝까지 파고들기'다. 한 정점을 시작으로 하여, 현재 있는 정점과 연결되어 있는 방문하지 않은 정점 중 하나에 들어가며 경로를 탐색하는 과정을 막다른 점에 도달할 때까지 반복하는 것이다. 막다른 점에 도달하면 왔던 경로를 다시 되짚어가다, 이동할 수 있는 정점이 발견되면 다시 탐색 과정을 반복한다. 조금 추상적으로 표현하면, 시작점을 표현하는 그래프의 각 '줄기'(경로)들을 순차적으로 내려가면서 특정한 점 등을 찾는 알고리즘이다.
이 과정을 그래프로 시각적으로 확인해보자.
시작
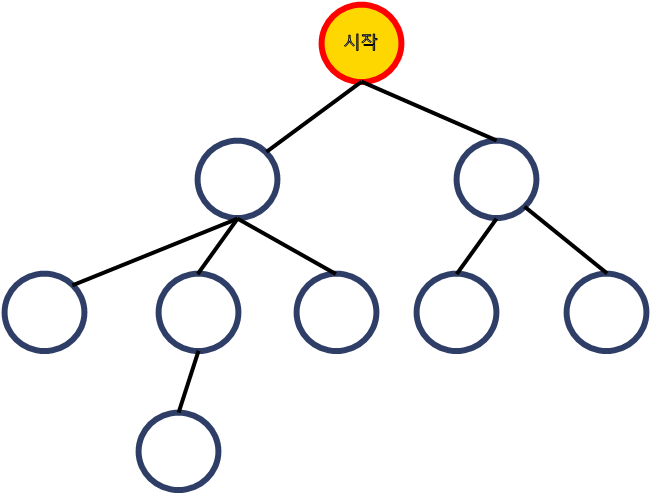
갈 수 있는 점이 여러 개 있는 상황에서, "왼쪽 점부터 방문하기"로 규칙을 정하자.
시작

내려갈 수 있는 점이 3개 있다. 역시 왼쪽부터 탐색한다.
시작
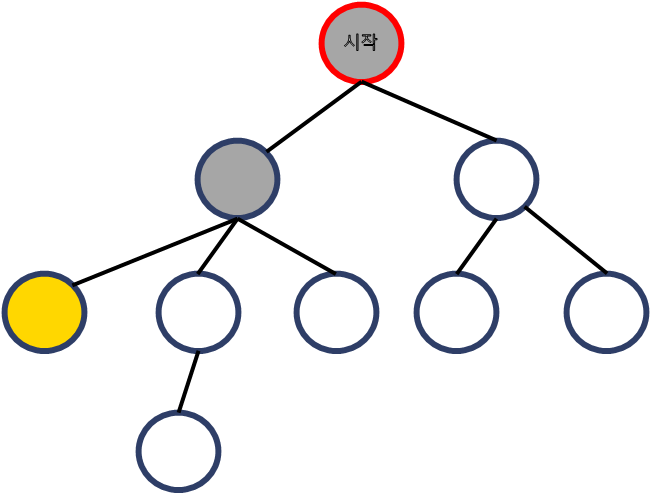
더이상 내려갈 수 없으니 바로 위로 돌아간다.
시작

그다음으로 방문하지 않은 두 점 중 왼쪽에 있는 점을 탐색한다.
시작

더 깊이 갈 수 있으니 탐색을 이어간다.시작
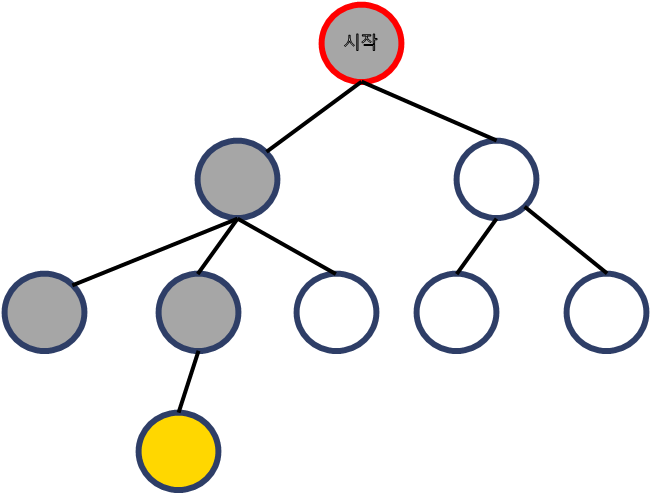
갈 수 있는 점이 더 없으므로 더 탐색할 수 있는 점이 있는 점까지 올라간다.
시작

시작

이제 갈 수 있는 점은 하나 남았으니 그 방향으로 탐색을 해본다.
시작

시작
다시 탐색을 계속할 점을 찾아 돌아온다.

시작

시작
시작점에 돌아왔다. 처음에 방문하지 않은 점으로 간다.

이후로도 같은 방법으로 탐색을 이어간다.
시작

시작

시작

시작

시작

다시 시작점으로 돌아왔다. 시작점에서 더이상 방문할 수 있는 점이 없으므로 탐색은 종료된다.
(다만, 특정한 정점을 찾는 알고리즘에서 사용된 DFS라면 원하는 정점을 찾았을 때 탐색을 종료하는 방법으로 보통 코드를 구성한다.)
실제로 코드를 작성할 때, 점들을 타고 깊이 내려가는 것은 그 정도가 정해지지 않은 반복 작업 이므로 이동하고 있는 경로를 간접적으로라도 저장하기 위해 재귀함수를 사용할 수 있다. 또한, 스택을 사용해서 직접적으로 경로를 저장하고 스택에 방문하는 노드를 저장하고 되돌아갈때는 다시 빼가는 방법으로 구현할 수도 있다.
의사 코드로 위 알고리즘을 재귀함수를 이용하여 간략히 작성해보면 다음과 같다.
def DFS(현재 노드 번호 K):
K = 목표 정점이라면:
함수 종료
i에 모든 정점을 대입해가며:
정점 i와 K가 연결되어있고/정점 i를 방문하지 않았다면:
i를 방문했다고 표시
DFS(i)
함수 종료정점 k의 방문을 DFS(k)의 실행으로 정의한다면, 한 정점을 방문한 뒤 그와 연결된 정점 중 방문하지 않은 정점을 방문하도록 재귀함수를 실행하면서 순차적으로 점들을 방문하는 것을 구현할 수 있었다. 또, 한 정점에서 방문할 수 있는 모든 정점들을 다 방문한 이후에는 해당 정점을 다루는 함수가 종료되면서 그 선두 정점을 다루는 함수로 다시 프로그램 작동 과정이 넘어가게 된다. 이와 같은 방식으로 DFS에서 정점 방문 과정을 구현할 수 있다.
깊이 우선 탐색은 그래프 전체를 구석구석 들어가며 탐색하는 방식으로, 특정한 정점을 찾아내거나 그래프의 구조(루프 구조 등)를 파악할 때 유용하게 사용할 수 있다.
'컴퓨터과학' 카테고리의 다른 글
| 자료구조_우선순위 큐 (0) | 2023.02.05 |
|---|---|
| 플로이드-워셜 알고리즘 증명 (0) | 2023.01.30 |
| 알고리즘_플로이드-워셜 알고리즘 (0) | 2023.01.29 |
| 군론 공부 5_ 준동형사상의 기본 정리 (0) | 2023.01.26 |
| 알고리즘_BFS(너비우선탐색) (0) | 2022.12.19 |
